Разделы сайта
- Главная
- Электроника: интересно и познавательно
- Организация производства радиоэлектронной техники
- Телефонные переговоры по технологии IP-телефонии
- Информационно-компьютерная система службы видеонаблюдения
- Физические основы электроники
- Автоматические системы управления
- Цифровые устройства и приемники
Исследование и расчет цепей синусоидального тока
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону:
![]() ,
,
где ![]() - максимальное значение или амплитуда
тока;
- максимальное значение или амплитуда
тока;
![]() -
угловая частота
-
угловая частота
![]() -
полная фаза колебания;
-
полная фаза колебания;
![]() -
начальная фаза.
-
начальная фаза.
Угловая частота ![]() ,
частота
,
частота ![]() и период T связаны соотношением:
и период T связаны соотношением:
![]()
![]() .
.
Проекция вращающегося против часовой стрелки с постоянной угловой
скоростью ![]() вектора
вектора ![]() на
вертикальную ось изменяется во времени по синусоидальному закону. Поэтому любая
синусоидальная функция (ток, напряжение, ЭДС) может быть изображена вектором.
на
вертикальную ось изменяется во времени по синусоидальному закону. Поэтому любая
синусоидальная функция (ток, напряжение, ЭДС) может быть изображена вектором.
При проведении расчета очень удобным оказывается рассмотрение
вращающегося вектора ![]() на комплексной плоскости. В этом случае
вектор
на комплексной плоскости. В этом случае
вектор ![]() можно представить как комплексную
амплитуду тока
можно представить как комплексную
амплитуду тока ![]() , а сам синусоидально изменяющийся ток I -
как мнимую часть произведения комплексной амплитуды на
, а сам синусоидально изменяющийся ток I -
как мнимую часть произведения комплексной амплитуды на ![]() :
:
![]() .
.
Тогда при t=0 можно записать:
![]() .
.
синусоидальный переменный ток
На практике широкое распространение получил символический метод расчета цепей синусоидального тока.
Сущность данного метода состоит в том, что при синусоидальном токе
можно перейти от дифференциальных уравнений, составленных для мгновенных
значений, к алгебраическим, составленным относительно комплексов амплитудных
значений тока ![]() , напряжения
, напряжения ![]() , и ЭДС
, и ЭДС ![]() либо
их действующих значений
либо
их действующих значений ![]() ,
, ![]() и
и
![]() . Например, если
. Например, если
![]() ,
,
то комплексное действующее значение напряжения
![]() ,
,
где ![]() .
.
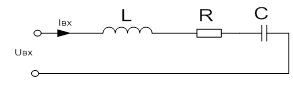
Рис. 1 Схема цепи с реактивными элементами
Аналогично осуществляется запись комплексов действующих значений величин ЭДС и тока. Например, для схемы (рис. 1) уравнение для мгновенных значений напряжений, составленное по второму закону Кирхгофа, запишется следующим образом:
![]() ,
или
,
или ![]() .
.
Переходя к комплексным действующим значениям напряжений, получим:
![]() ,
,
где R - активное сопротивление цепи,
![]() -
комплексное индуктивное сопротивление цепи,
-
комплексное индуктивное сопротивление цепи,
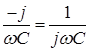 -
комплексное емкостное сопротивление цепи.
-
комплексное емкостное сопротивление цепи.
Множитель ![]() свидетельствует о том, что вектор
напряжения
свидетельствует о том, что вектор
напряжения ![]() на индуктивности L опережает вектор тока
на индуктивности L опережает вектор тока ![]() на
на ![]() .
Множитель
.
Множитель ![]() свидетельствует о том, что вектор
напряжения
свидетельствует о том, что вектор
напряжения ![]() на емкости С отстает от вектора тока
на емкости С отстает от вектора тока ![]() на
на ![]() .
На активном сопротивлении R векторы напряжения
.
На активном сопротивлении R векторы напряжения ![]() и
тока
и
тока ![]() совпадают по направлению.
совпадают по направлению.
Величина ![]() называется комплексным сопротивлением
цепи (см. рис. 1.2), а
называется комплексным сопротивлением
цепи (см. рис. 1.2), а 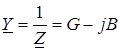 - ее комплексной проводимостью, где G и B
- активная и реактивная составляющие проводимости цепи.
- ее комплексной проводимостью, где G и B
- активная и реактивная составляющие проводимости цепи.
Комплексные числа записываются в одной из следующих форм:
алгебраическая - ![]() ;
;
показательная - ![]() ;
;
тригонометрическая - ![]() ;
;
полярная - ![]() .
.
Геометрически любому комплексному числу ![]() можно сопоставить в соответствие точку
комплексной плоскости
можно сопоставить в соответствие точку
комплексной плоскости ![]() с координатами x=a, y=jb или
радиус-вектор длиной A единиц, проведенный из начала координат в точку A и
расположенный под углом
с координатами x=a, y=jb или
радиус-вектор длиной A единиц, проведенный из начала координат в точку A и
расположенный под углом ![]() к оси абсцисс (рис. 1.3). Из рисунка
очевидны формулы перехода из одной формы записи комплексного числа к другой:
к оси абсцисс (рис. 1.3). Из рисунка
очевидны формулы перехода из одной формы записи комплексного числа к другой:
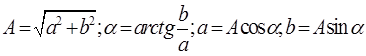
Алгебраическая форма применяется при сложении и вычитании
комплексных чисел, а показательная - при умножении, делении, возведении в
степень и извлечении корня. Умножении числа на мнимую единицу ![]() сводится к повороту вектора на угол 900
против часовой стрелки, умножение на
сводится к повороту вектора на угол 900
против часовой стрелки, умножение на ![]() -
к повороту на угол 900 по часовой стрелке, а умножение на -I
соответствует повороту на
-
к повороту на угол 900 по часовой стрелке, а умножение на -I
соответствует повороту на ![]() .
.
Полное комплексное сопротивление цепи ![]() и сопротивления ее участков (R, L и С)
геометрически связаны треугольником сопротивлений:
и сопротивления ее участков (R, L и С)
геометрически связаны треугольником сопротивлений:
а) если ![]() , то
, то ![]()
б) если ![]() , то
, то ![]() ,
где
,
где ![]()
Расчет электрической цепи в комплексной форме требует записи одного и того же комплексного числа в алгебраической и показательной формах.
Рассмотрим несколько примеров.
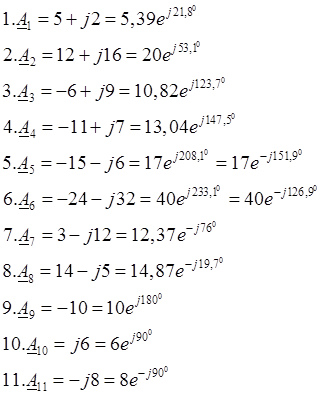
- Векторные диаграммы
- Цепи с индуктивно связанными элементами
- Исследование элементов цепи в отдельности
- Исследование цепи с элементами, соединенными последовательно
- Исследование цепи со смешанно соединенными элементами
- Исследование цепей с взаимной индукцией
- Исследование явления резонанса напряжений в электрических цепях
Интересное из раздела
Амплитудная модуляция
Исследование
различных видов модуляции необходимо для определения требуемых свойств каналов,
сокращения избыточности модулированных сигналов и улучшения исп ...
Проектирование автомата подачи звонков
Разработанный автомат подачи звонков удовлетворяет всем
требованиям, предъявленным в задании. Настройка автомата производится с помощью
трех кнопок: «вверх» ...
Усилитель низкой частоты для наушников
За последние 100 лет, значительные изменения во многих областях
науки и техники обусловлены быстрым развитием электроники. На сегодняшний день
невозможно на ...