Избыточность и цифровая коррекция

Для построения конвейерного АЦП с большой устойчивостью к ошибкам, вводится избыточность, представляющая собой сумму результатов отдельных уровней, большую, чем общее разрешение. Эта избыточность используется для устранения нелинейности и межкаскадного смещения аналого-цифрового преобразователя (ADSC) с помощью алгоритма цифровой коррекции. В большинстве предыдущих реализаций цифровых алгоритмов коррекции для исправления ошибок используется как сложение, так и вычитание. При таком подходе есть две проблемы. Во-первых, такой способ сложнее проверить, поскольку такая логика имеет три стадии (сложение, вычитание, отсутствие действий) и ни один из этих этапов не обязателен для выходного кода. В результате, отсутствует возможность проверить каждый этап путем изучения исправленного сигнала с выхода АЦП. Таким образом, удовлетворительные результаты функционального тестирования АЦП еще не гарантируют безотказной логики коррекции. Например, во время функционального тестирования, АЦП может содержать набор признаков сравнения, которые заставляют коррекционную логику выполнять только сложение. Тогда присутствие в корректирующей логике неисправностей было бы не обнаружено при тестировании. Если эти после функционального тестирования изменится набор признаков, при котором должно выполняться вычитание, незамеченные неисправности могут привести к тому, что на выходе АЦП сигнал будет неверный. Поэтому, что бы проверить наличие ошибок в логике коррекции тщательно, тестовые векторы должны быть введены непосредственно в логику, минуя АЦП. Во-вторых, данный подход является излишне сложным, так как вычитание эквивалентно сложению с отрицательным значением, поэтому необходимость в вычитания отпадает путем создания необходимого смещения в ADSC и ЦАП.

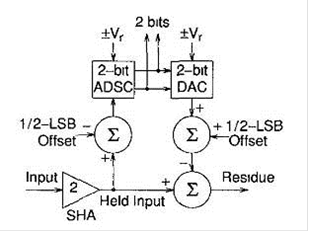
Рисунок 2 - Блок-схема одного уровня с ADSC и ЦАП

На рис. 2 показано блок-схема одного уровня конвейерного АЦП со смещением в АЦП и ЦАП. Этап 2-b используется в качестве представительного примера. Обе величины смещения равны ½ младшего значащего разряда (Vr/4, где полномасштабный сигнал АЦП равен ± Vr)

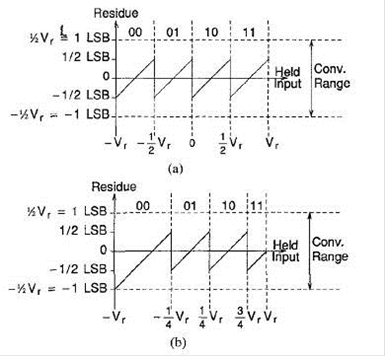
Рисунок 3 - Идеальный остаток от сигнала принятый а) без задержки б) с задержкой

равномерно сдвигает график каждого отдельного участка определенного уровня вправо, а ЦАП сдвигает весь график вниз. Поскольку в половине шкалы на рис 3 б нет сигнала, то у каждого уровня многоуровневого АЦП будет довольно таки хорошая передаточная характеристика на половине шкалы.

Пусть диапазон коррекции можно определить как сумму всех определенных уровней, сдвинутых так, что бы быть устойчивыми к ошибкам. Если ЦАП и схема выборки/хранения идеальные, и межуровневое усиление равно 2, то усиленный остаток остается в пределах диапазона преобразования на следующем уровне, когда нелинейность ADSC сдвигает уровни не более, чем на ±1/2 уровня младшего значащего символа но уровне 2-б. При таких условиях ошибки, вызванные нелинейностью ADSC, могут быть исправлены, поэтому диапазон исправления здесь ±1/2 LSB или ± Vr/4, что означает, что линейность ADSC должна быть соизмерима с отдельными отсчетами, а не со всем разрешением АЦП. Кроме того, так как линия задержки, показанная на рисунке 2, сдвигает сигнал вправо на величину задержки, то цифровой сигнал на выходе всегда будет меньше или эквивалентен его идеальной форме если нелинейность ADSC может сдвинуть сигнал назад влево не больше, чем на эту же величину. Таким образом, коррекция требует либо отсутствие изменений, либо увеличения. Поскольку соответствующей коррекционной логике не нужно делать вычитание, то ее легче проверить, чем обычную логику цифровой коррекции. Однако, так как оба оставшихся варианта не обязательно могут произойти во время функционального теста АЦП, то проверка логики коррекции все еще проблематична.

Хотя идеальный остаток (рис. 3а) всегда находится в промежутке ± Vr/4, на рис. 3б он находится в промежутке от - Vr/2 до Vr/4. С одинаковыми уровнями и межкаскадным усилением равным 2, минимальный остаток (рис. 3б) получается на левом конце графика и лежит на нижнем уровне преобразования границы следующего уровня АЦП. Несмотря на то, что сдвиг уровня сигнала никак не влияет на значение остатка на левом конце графика, межкаскадное смещение или ошибка усиления могут вызвать смещение графика на левом конце ниже диапазона преобразования следующего уровня. Влияние этих факторов на линейность АЦП будет представлена дальше.

Межкаскадная ошибка задержки сдвигает весь график и это эквивалентно комбинации двух смещений на предыдущем этапе: ответвление сигнала и изменение полярности. Если диапазон коррекции не превышает комбинацию этих смещений в АЦП, и нелинейность в АЦП устраняет эффект смещения при цифровой коррекции, относя входное смещение только к межкаскадному смещению. Начиная с диапазона коррекции отсчеты сдвигаются так, чтобы быть устойчивыми к ошибке и, начиная с уровня левого конца графика, остаток не зависел от бы от перемещения отсчетов. Поэтому, увеличенный остаток в левом конце графика (рис. 3б) (по сравнению с рис. 3а) не увеличивает чувствительность к изменению линейности между уровнями.

Интересное из раздела

Модернизация сети широкополосного доступа оператора связи ООО ТомГейт
Информационные методы все шире внедряются во все сферы деятельности. Информатизация, конвергенция компьютерных и телекоммуникационных технологий, переход к ...

Прибор для мониторинга напряжения питающей сети
устройство электронный измерительный индикация С уровнем развития энергетики часто связывают состояние промышленного производства, уровень жизни населения и ...

Расчет токовой защиты нулевой последовательности
Задание и исходные данные Произвести расчет дистанционной защиты линии и начертить карту селективности дистанционных защит. Исходные данные: ...