Исследование алгоритмов цифровой обработки сигналов

Из теории аналоговых фильтров известно, что сигнал Sv(t) на выходе фильтра выражается в виде свертки

где h(t) - импульсная характеристика фильтра (напоминаем - отклик фильтра на дельта-функцию ); S(t-τ) - входной сигнал.

При реализации цифровых фильтров используется дискретная свертка

где h(kT) - дискретные значения (цифровые) импульсной характеристики фильтра; S[(n-k)T]- дискретные (цифровые) значения задержанного на k тактов входного сигнала.

Для вычисления дискретной свертки можно использовать дискретное преобразование Фурье (ДПФ). Для этого необходимо выполнить следующие действия:

. Вычислить ДПФ входного сигнала:

где Ω=2π/NT - основная частота преобразования, exp(-jΩT) = exp(-j2π/N) - отсчеты дискретной экспоненты, которая называется поворачивающим множителем, С(kΩ)=C(k) - коэффициенты ряда Фурье, число коэффициентов ряда равно числу отсчетов (N) дискретного сигнала.

. Вычислить ДПФ дискретной импульсной характеристики

3. Перемножить коэффициенты полученных ДПФ

4. Вычислить обратное ДПФ от G(kΩ)

Исследование свойств дискретной свертки

Сигнал S(nT) периодический [1, 4, 2, 3] с периодом N=4 (рис. 1).

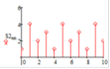
Рис. 1

Импульсная характеристика h(nT) периодическая [0, 1, 0, 0] с периодом N=4 (рис. 2).

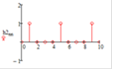
Рис. 2

Определим круговую свертку в соответствии с выражением (1) (рис. 3).

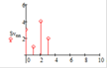
Рис. 3

Исследование работы цифрового фильтра без помехи

Цифровой фильтр (ЦФ) представляет собой цифровое устройство или алгоритм обработки сигнала, реализованный программно на ЭВМ. Математически работа цифрового фильтра описывается уравнением в конечных разностях

где am и bk - коэффициенты, определяемые задачами обработки сигнала.

В теории цифровой обработки синтезирован фильтр, минимизирующий среднеквадратичное отклонение. Структурная схема фильтра приведена на рис. 4.

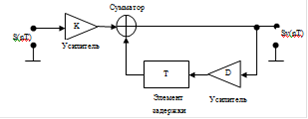
Рис. 4

К, D - коэффициенты усиления, определяемые параметрами аддитивной смеси.

Алгоритм работы фильтра программно реализуется в соответствие с выражением

где

Для оценки качества фильтра используют среднеквадратическое отклонение, которое определяется по формуле

Пусть сигнал Sign(t) - прямоугольный импульс (рис. 5)

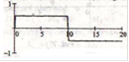
Рис. 5

Его дискретное представление изображено на рис. 6.

Рис. 6

Интервал дискретизации Т=1.

Отклик фильтра на заданный сигнал представлен на рис. 7.

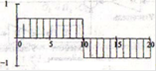
Рис. 7

Для данного случая СКО равно σ = 5.4*10-3.

Исследуем работу цифрового фильтра, если на входе произвольный сигнал, представленный на рис. 8.

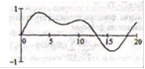
Рис. 8

Дискретное представление сигнала изображено на рис. 9.

Рис. 9

Интервал дискретизации T = 1.

Для данного случая СКО равно σ = 4.2*10-3

Исследование работы цифрового фильтра при наличии помехи

Пусть сигнал - произвольной формы (рис. 10).

Рис. 10

Интересное из раздела

Ошибки позиционирования GPS-приемников в условиях полярных геомагнитных возмущений
Определение своего положения с помощью GPS навигатора, отдельного прибора, или устройства, встроенного в карманный компьютер или сотовый тел ...

Организация технологической железнодорожной связи
Дальнейшее повышение эффективности и качества грузовых и пассажирских перевозок требует максимального использования достижений науки и техники и широкого вн ...

Расчет характеристик сигналов и каналов связи
В последнее десятилетие ХХ века произошла научно-техническая революция в области транспортной связи, в основе которой лежат два крупных достижения ...