Оценка устойчивости САР на основе критерия Найквиста

Для оценки устойчивости САР необходимо воспользоваться передаточной функцией разомкнутой системы и, заменяя s → jω, построить годограф амплитудно-фазовой частотной характеристики (АФЧХ). Особенностью данного критерия является то, что по виду АФЧХ разомкнутой системы оценивается устойчивость САР в замкнутом состоянии.

Система автоматического управления в разомкнутом состоянии может быть устойчивой, неустойчивой или нейтральной. Поэтому существует два подхода в оценке устойчивости системы.

Если система в разомкнутом состоянии устойчивая

, то для того, что бы она была устойчивой и в замкнутом состоянии, необходимо и достаточно чтобы годограф АФЧХ разомкнутой системы не охватывал точку с координатами [-1; j0].

Если годограф АФЧХ разомкнутой системы проходит через точку с координатами [-1; j0], то система в замкнутом состоянии является нейтральной, то есть находится на границе устойчивости.

На рис.7.1 представлены годографы АФЧХ трех САР. Годограф 1 соответствует САР, устойчивой в замкнутом состоянии, 2 - нейтральной, 3 - неустойчивой.

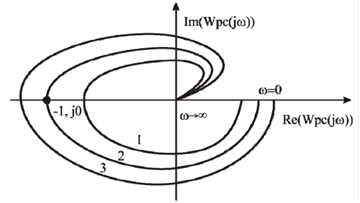
Рис.7.1 Годографы АФЧХ разомкнутой системы

Если система в разомкнутом состоянии является неустойчивой или нейтральной.

(В характеристическом уравнении разомкнутой системы среди левых корней имеется хотя бы один правый корень или нулевой), то для того, что бы она была устойчивой в замкнутом состоянии, необходимо и достаточно чтобы годограф АФЧХ разомкнутой системы охватывал точку с координатами [-1; j0] в положительном направлении К/2 раз, где К - количество правых корней разомкнутой системы.

На рис. 7.2 изображен годограф АФЧХ неустойчивой разомкнутой системы, которая имеет один правый корень.

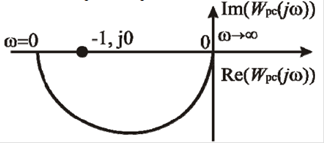
Рис. 7.2 Годограф АФЧХ разомкнутой системы при К=1

Годограф АФЧХ охватывает точку с координатами [-1; j0] в положительном направлении 0,5 раза, следовательно, система в замкнутом состоянии является устойчивой.

Оценим устойчивость САР следящей системы, используя критерий Найквиста.

Воспользуемся передаточной функцией САР следящей системы.

WРС(S)= · KЭУ· · · KДН· KУ2=

= =

= =

= =

=

Определим корни характеристического уравнения разомкнутой системы, используя Matlab.

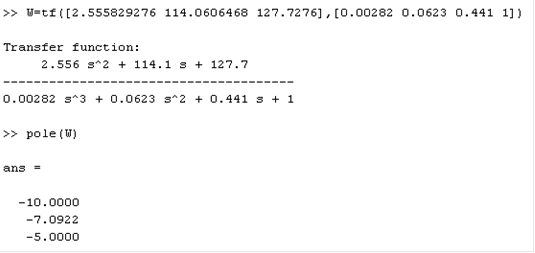
Так как все корни левые, используем 1-й

подход оценки устойчивости системы.

Используя Mathсad, построим годограф АФЧХ устойчивой разомкнутой системы (рис. 7.3 и рис. 7.4).

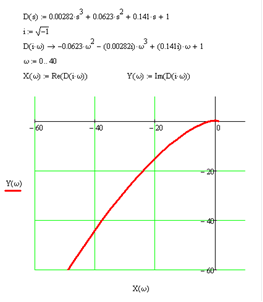
Рис. 7.3 Годограф кривой Найквиста дляω от 0 до 40 (с-1)

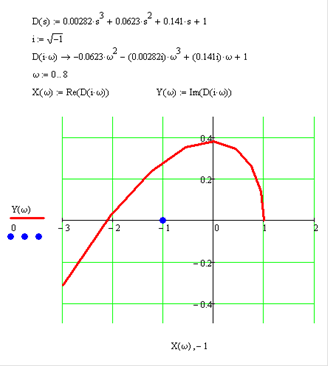
Рис. 7.4 Годограф кривой Найквиста дляω от 0 до 8 (с-1)

Вывод:

Годограф кривой Найквиста, согласно рис. 7.4, охватывает точку скоординатами [-1; j0], следовательно, система в замкнутом состоянии являетсяустойчивой.

Интересное из раздела

Цифровой УКВ-приемник
В последние несколько лет заметна тенденция резкого сокращения сроков проектирования новых изделий при все возрастающих требованиях к их качественным характеристикам. Это ...

Цифровой КИХ-фильтр для частотной селекции измерительных сигналов
Цифровой фильтр (ЦФ) - устройство, пропускающее, либо подавляющее заданные в цифровой форме сигналы в определенной полосе частот. В отличие от аналоговых фильтров, у кото ...

Генератор цифровых тестовых сигналов
Ускорение научно-технического прогресса, развитие автоматизации процессов производства требует постоянного совершенствования систем сбора и переработки информации. Наибол ...