Определить полную установившуюся ошибку системы

Исследование точности регулирования систем автоматического управления проводят путем анализа функционирования ее установившихся режимов. То есть, точность регулирования системы оценивается установившимися ошибками, которые в свою очередь определяются структурой системы (передаточными функциями) и воздействиями (задающими воздействиям и возмущающими факторами).

В следящих системах автоматического управления и следящем приводе задающее воздействие изменяется с постоянной скоростью υ0.

g(t)= υ0·t, υ0 = const

либо с постоянным ускорением

Точность процесса регулирования оценивается с помощью ряда ошибок

где εycm(t) -установившаяся ошибка;

c0, c1,…,cn/n! -коэффициенты ряда ошибок;

g’(t), g’’(t), dng(t)/dtn- 1-я, 2-я, …, n-я производные от задающего воздействия.

Коэффициенты c0, c1,…, cn/n! ряда ошибок выражаются через передаточную функцию по ошибке регулирования следующим образом:

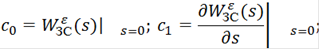
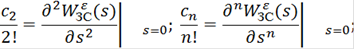
Ряд ошибок на практике является ограниченным как справа, так и слева. Ограниченность справа обуславливается равенством нулю некоторых производных от задающего воздействия g(t). Так, например, при типовом воздействии g(t)= g0 ·1(t) установившаяся ошибка определяется по выражению

εycm= c0 · g0

В этом случае коэффициент ряда ошибок c0 характеризует статическую ошибку

.

Если задающее воздействие изменяется с постоянной скоростью, установившаяся ошибка выражается как

εycm= c0 · υ0 ·t + c1 · υ0

где коэффициент c

1

характеризует ошибку по скорости.

Установившаяся ошибка для задающего воздействия выражается как

Коэффициент c2 /2!характеризует ошибку по ускорению.

Из выражений представленных выше выражений следует, что для устранения статической ошибки, ошибок по скорости и ускорению необходимо равенство нулю, соответственно, коэффициентов c0, c1, c2 /2!. Для этого необходимо обеспечить системе соответствующий порядок астатизма.

Под порядком астатизма понимается степень υ изображения Sυ, находящегося в знаменателе передаточной функции разомкнутой системы.

Например для

порядок астатизма равен 2.

Для астатических систем1-го порядка коэффициент c0 равен нулю, для систем с астатизмом 2-го порядка - c0, c1равны нулю, для систем с астатизмом3-го порядка - c0, c1, c2 /2! равны нулю. Таким образом, астатические системы 1-го порядка воспроизводят без ошибки постоянные задающие воздействия

g(t)= g0 ·1(t)

системы с астатизмом 2-го порядка воспроизводят без ошибки задающее воздействие, меняющееся с постоянной скоростью

g(t)= υ0 ·t, υ0 = const

и т. д.

Выражение для передаточной функции:

Заключение

В ходе выполнения данной курсовой работы были закреплены знания, полученные на лабораторных занятиях, в процессе самостоятельного изучения специальной литературы. Был приобретен опыт работы с пакетами прикладных программ и системами автоматизированного проектирования систем управления, а также приобретен навык самостоятельной исследовательской работы.

Интересное из раздела

Функционально-логическое проектирование цифрового узла заданного типа в заданном базисе и проверка его функционирования при различных наборах воздействующих сигналов
Цель работы: синтезировать цифровой узел заданного типа в заданном базисе и проверить его функционирование при различных наборах воздействующих сигналов. ...

Цифровой КИХ-фильтр для частотной селекции измерительных сигналов
Цифровой фильтр (ЦФ) - устройство, пропускающее, либо подавляющее заданные в цифровой форме сигналы в определенной полосе частот. В отличие от аналоговых фильтров, у кото ...

Ошибки позиционирования GPS-приемников в условиях полярных геомагнитных возмущений
Определение своего положения с помощью GPS навигатора, отдельного прибора, или устройства, встроенного в карманный компьютер или сотовый тел ...