Модели цифровых сигналов

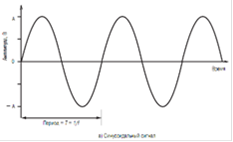
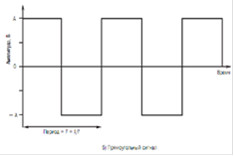
Рис. 2.4. Периодические сигналы

По горизонтальной оси на рис 2.5 отложено время; на самом же графике показана зависимость от времени величины сигнала в данной точке пространства. Подобные графики (с точностью до изменения масштаба) можно получить, если отложить на горизонтальной оси расстояние. В этом случае на графике будет изображена интенсивность сигнала в данный момент времени в зависимости от расстояния. Например, при передаче синусоидальной волны (если рассмотреть электромагнитную волну на некотором расстоянии от антенны или звук на некотором расстоянии от громкоговорителя) в отдельный момент времени интенсивность сигнала изменяется по гармоническому закону как функция расстояния от источника.

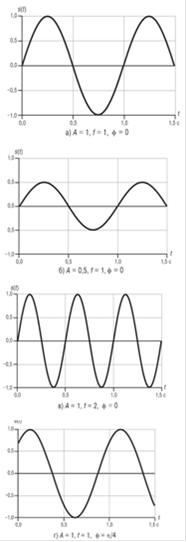
Рис. 2.5. s(t)=A sin (2πf t + φ)

Существует простое соотношение между двумя синусоидальными сигналами, один из которых изменяется во времени, а другой − в пространстве. Определим длину волны сигнала λ, как расстояние, занимаемое одним периодом или, иными словами, как расстояние между двумя точками равных фаз двух последовательных циклов. Предположим, что сигнал распространяется со скоростью ν. Тогда длина волны связана с периодом следующим соотношением: λ = νТ, что равносильно λf = ν. Особое значение для нашего изложения имеет случай ν = c, где c - Скорость света в вакууме, приблизительно равная

Основные понятия частотного представления сигнала

Реальный электромагнитный сигнал составлен из многих частот. Рассмотрим, например, сигнал, показанный на рис. 2.6, в.

S(t)=(4/π)×[sin(2πft)+(1/3)sin(2π(3f)t)] (2.3)

Он состоит из простых синусоидальных сигналов с частотами f и 3f, показанных соответственно на рис. 2.6, а и б. Отметим два интересных момента, связанных с этим рисунком.

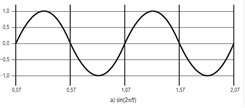
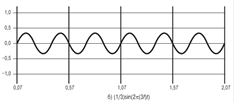
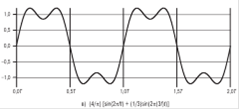
Рис. 2.6. Сложение частотных составляющих (Т = 1/f)

Вторая частота кратна первой. Если все частотные составляющие сигнала кратны одной частоте, то последняя называется собственной частотой.

Период суммарного сигнала равен периоду сигнала собственной частоты. Период составляющей sin (2πƒt) равен Т = 1/ƒ, и, как можно увидеть на рис. 2.6, в, период сигнала s(t) также равен Т.

Любой сигнал складывается из синусоидальных составляющих с разными частотами. Сложив вместе достаточное количество синусоидальных сигналов с соответствующими амплитудами, частотами и фазами, можно получить электромагнитный сигнал любой формы. Аналогично любой электромагнитный сигнал рассматривается как совокупность периодических аналоговых (синусоидальных) сигналов с разными амплитудами, частотами и фазами. Далее по ходу изложения мы увидим, как важно иметь возможность рассмотреть сигнал не как процесс изменения во времени (временное представление), а как функцию частоты (частотное представление).

Спектром сигнала называется область частот, составляющих данный сигнал. Для сигнала, приведенного на рис. 2.6, в, спектр простирается от ƒ до 3ƒ. Абсолютной шириной полосы сигнала называется ширина его спектра. В рассматриваемом случае (рис. 2.6. в) ширина полосы составляет 3ƒ-ƒ=2ƒ. Многие сигналы имеют бесконечную ширину полосы, но большая часть их энергии сосредоточена в относительно узкой полосе частот, называемой эффективной полосой, или просто полосой.

Интересное из раздела

Компьютерные сети
Компьютеры уже прочно вошли в современный мир, во все сферы человеческой деятельности и науки, тем самым создавая необходимость в обеспечении их различн ...

Проектирование автомата подачи звонков
Разработанный автомат подачи звонков удовлетворяет всем требованиям, предъявленным в задании. Настройка автомата производится с помощью трех кнопок: «вверх» ...

Автоматическая система управления
В настоящее время широко используются микропроцессорные устройства и системы. Их назначение и область применения очень велика. Так, различного рода микропроцессорные сист ...