Определение интервала дискритизации и разрядности кода

Дальнейший расчет ведем для сигнала заданного экспоненциальное т.к. у этого сигнала частота среза оказалась меньше чем у других.

wс=35536 рад/с.

Интервал дискретизации Dt по времени определяем на основе теоремы Котельникова по неравенству:

Dt £ 1/(2×Fв), (2.1)

где Fв=wс/(2×p) - верхнее значение частоты спектра сигнала.

в=35536/2×p=5.66×103 Гц

Dt=1/5.66×103×4=4.42×10-5 с.

Необходимо, чтобы сигнал был представлен не менее чем четырьмя отсчетами.

д=1/Dt=1/4.42×10-5 =22640Гц.

График дискретизированного по времени сигнала

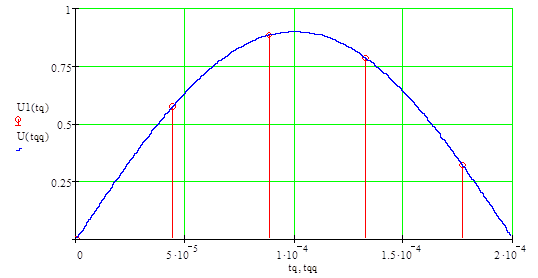
Рис. 2.1

Следующими этапами преобразования сигнала являются квантование импульсных отсчетов по уровню и кодирование.

Разрядность кода определяется исходя из динамического диапазона квантуемых по уровню импульсных отсчетов. При этом в качестве верхней границы динамического диапазона Umax принимается напряжение самого большого по амплитуде отсчета. Umax=0.9 В.

Нижняя граница диапазона:

=Umax/K; (2.2)

- заданный коэффициент.=0.9/20=0.045 В;

g=35.

Дальнейший расчет ведем следующим образом.

Известно, что:

кв=D2/12; D - шаг шкалы квантования.

D=Umax/nкв;

кв - число уровней квантования.

Отсюда:

;

При использовании двоичного кодирования:кв = 2m; m - разрядность кодовых комбинаций.

= log nкв;= log 34= 6.

Длительность элементарного кодового импульса t определяется исходя из интервала дискретизации Dt и разрядности кода m. Здесь необходимо ввести защитный интервал, под который отведем половину Dt. В итоге получим выражение:

tи= Dt/(2×m); (2.3)

tи = 4.42×10-5 /12 =3.68×10-6мкс.

Для разработки математической модели цифрового сигнала примем четыре кодовых слова (коды четырех отсчетов). Числовые константы сигнала определяются по формулам (2.4) и (2.5). Математическое ожидание:

. (2.4)

Дисперсия:

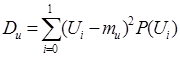. (2.5)

Выбранная кодовая последовательность:

Вероятность нуля:

Вероятность единицы:

Рассчитаем математическое ожидание сигнала по (2.8).

В.

Дисперсия:

В.

Рассчитаем функцию автокорреляции. При проведении расчетов воспользуемся возможностями программы MathCAD. Поступим следующим образом. Выпишем четыре последовательности кодов, которыми представляется дискретизированный сигнал; это будет последовательность нулей и единиц.

В среде MathCAD. создадим два вектора и . Далее воспользуемся функцией . После каждого измерения будем сдвигать кодовую последовательность вектора Vy на один знак. Проведём семь расчётов. Результаты занесём в таблицу 2.2

Таблица 2.1 - Функция автокорреляции кодового сигнала

Интересное из раздела

Расчет спектра и энергетических характеристик сигнала
В последнее десятилетие ХХ века произошла научно-техническая революция в области транспортной связи, в основе которой лежат два крупных достижения науки сер ...

Программируемый формирователь последовательности импульсов с цифровой индикацией количества импульсов
Проектируемое устройство в готовом виде представляет собой отдельный прибор, основной функцией которого является формирование последовательности импульсов заданной частот ...

Проектирование автоматического измерителя артериального давления
Важным компонентом клинического мониторинга, определяющим состояние сердечнососудистой системы и организма в целом, является контроль кровяного давления. Дв ...