Надежность технических систем

где вторая производная корреляционной функции, через которую выражается дисперсия скорости этого процесса

Если пределы Xн, Xв допустимого изменения параметра X являются неслучайными, то задача отыскания становится более простой. Для ее решения нужно знать только плотность вероятности f(x), если она известна, то

.

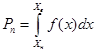Графически вероятность параметрической безотказности при детерминированных пределах работоспособного состояния можно изобразить так

Если случайный параметр X имеет нормальное распределение с плотностью

То задача сводится к отысканию величин табличной функции Ф0(x) (см. приложение)

С учетом того, что

Ф0(-x)=1- Ф0(x),

Вероятность процесса безотказной работы может быть вычислена по формуле:

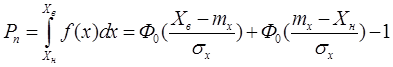
Решить задачу.

Дано: случайный процесс p(t) изменения давления в камере сгорания двигателя является стационарным нормальным с постоянным математическим ожиданием mp=5МПа и дисперсией sp2=0,0625 МПа2, а его корреляционная функция имеет вид

,

где a=0,015 с-1. Установлены неслучайные пределы - верхний pв=6МПа и нижний pн=4МПа, выход за которые рассматривается как параметрический отказ двигателя.

Проанализировать:

Влияние первичных отклонений на случайный процесс p(t) на основе анализа графика нормированной к sp2корреляционной функции Kp(t).

(при значениях параметра a=(0,015 с-1,0,0015 с-1, 0,0с-1)

Найти:

Вероятность того, что в течение t=100 cработы двигателя не произойдет ни одного выброса давления за уровни pв, pн, если выбросы за верхние и нижние уровни можно считать независимыми событиями.

Рассчитать вероятность параметрической безотказности в предположении, что его работоспособное состояние определяется одним параметром - давлением в камере сгорания - p. Длительность процесса не учитывать.

Сделать выводы, сравнивая результаты п.2 и п.1.

Решение:

Построим график нормированной к sp2корреляционной функции Kp(t)при значениях параметра a=(0,015 с-1,0,0015 с-1, 0,0с-1).

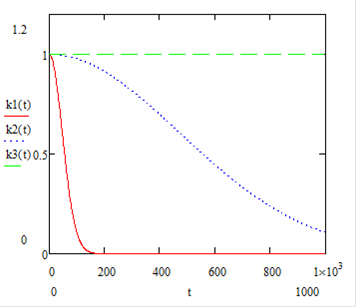
На этом графике:

k1(t) = exp(-0,015∙t2);k2(t) = exp(-0,0015∙t2);k3(t) = exp(-0,00∙t2);

надежность безотказный функция вероятность

Из представленных графиков видно, что влияние первичных отклонений на случайный процесс p(t) будет более значимым, если корреляционная функция постоянна и равна 1. Такое происходит при значении параметра a= 0. В этом случае случайный процесс определяется первичными отклонениями.

При росте параметра a первичные отклонения влияют на случайный процесс только в начальный момент времени, при этом с ростом параметра a это влияние уменьшается.

Найдем вероятность того, что в течение t=100 c работы двигателя не произойдет ни одного выброса давления за уровни PВ, PН, если выбросы за верхние и нижние уровни можно считать независимыми событиями.

Вероятность отсутствия выброса случайной стационарной функции за допустимые нижний и верхний пределы в течение времени t будет

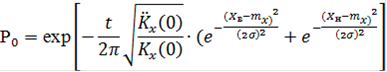
где вторая производная корреляционной функции, через которую выражается дисперсия скорости этого процесса

,

Подставим величины в формулу.

Kx(0) = sp2=0,0625 МПа2,

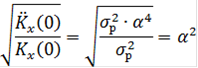
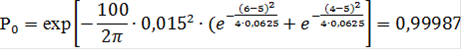
Рассчитаем вероятность параметрической безотказности в предположении, что его работоспособное состояние определяется одним параметром - давлением в камере сгорания - p. Длительность процесса не учитывать.

Вероятность процесса безотказной работы может быть вычислена по формуле:

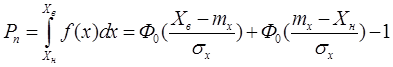
Ф(Х) - функция нормального распределения, ее значения приведены в таблице.

Интересное из раздела

Автоматизированная система учета энергоресурсов
Вследствие роста тарифов на энергоресурсы, потребляемые населением (газ, вода, электроэнергия), встает вопрос о необходимости оперативного и достоверного контро ...

Исследование входных цепей радиоприемников
Цель работы: Закрепление теоретических знаний и экспериментальное исследование входных цепей при емкостной, индуктивной и смешанной связи с ненастрое ...

Исследование узлов и систем автоматического регулирования
Объектом исследования данного курсового проекта является системы автоматического регулирования, их виды, элементарные звенья и их математические модели с те ...