Расчет характеристик осциллирующего сигнала

Временная функция сигнала имеет вид:

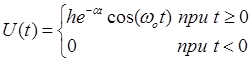. (1.9)

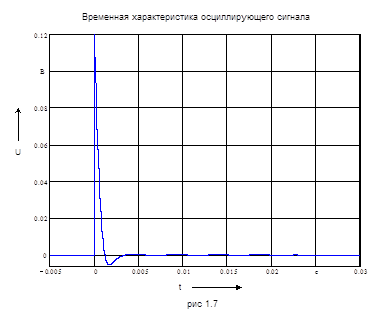
У заданного сигнала , график этого сигнала изображен на рис. 1.7.

Прямое преобразование Фурье для этой функции имеет вид

. (1.10)

учетом коэффициентов получаем:

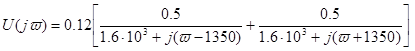В/Гц. (1.11)

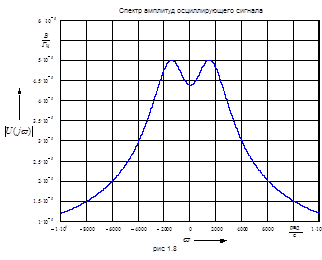
График амплитудного спектра U(w) изображен на рис. 1.8.

Спектр фаз можно определить применив функцию arg(х), получаем:

. (1.12)

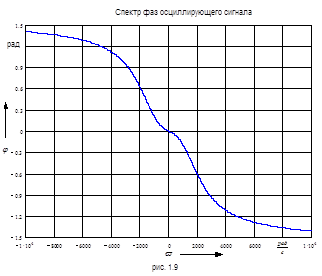
График спектра фаз функции изображен на рис. 1.9.

Расчет полной энергии и ограничение практической ширины спектра осциллирующего сигнала

Полная энергия сигнала (1.9) в общем случае рассчитывается по (1.3). Применив табличный интеграл, имеем:

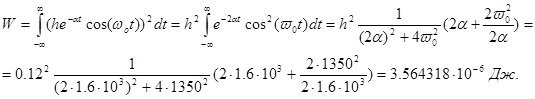
Ограничение практической ширины спектра сигнала по верхнему значению частоты wс осуществляется так же, как и для предыдущих сигналов.

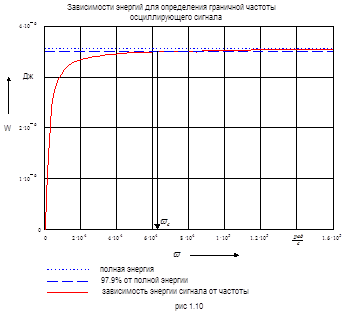
Для определения граничной частоты в одной системе координат построим график W`, прямые полной энергии W=3.564318×10-6 Дж и части полной энергии W``=d×W=3.489467×10-6 Дж. Находим значение wс по графику, изображенному на рис. 1.10. Точка пересечения W` и W`` соответствует значению wс.

wс=6.1×104 рад/с.

В данном разделе определены энергии трех сигналов и с учетом коэффициента d, определяющего процент полной энергии, проведен расчет граничной частоты, на основании чего можно выбрать для последующих расчетов экспоненциальный сигнал, т.к. у данного сигнала самый узкий спектр и к каналу, по которому будет передаваться этот сигнал, предъявляются менее жесткие требования.

Интересное из раздела

Проектирование блока горизонтального отклонения электронно-лучевого осциллографа
Электронно-лучевой осциллограф является наиболее универсальным измерительным прибором, позволяющим исследовать сложные электрические процессы, визуально наб ...

Прибор для мониторинга напряжения питающей сети
устройство электронный измерительный индикация С уровнем развития энергетики часто связывают состояние промышленного производства, уровень жизни населения и ...

Калибровка мониторов на основе науки о цвете – колориметрии
Полиграфическая индустрия активно развивается и предлагает клиентам все больше новых и интересных решений. Также растет требовательность заказчиков к резуль ...