Элементарные динамические звенья иих характеристика

Передаточные функции сложных динамических элементов можно представить в виде выражения, состоящего из произведений простых сомножителей первого или второго порядка. При анализе динамических свойств систем автоматического управления часто оказывается удобным вводить в рассмотрение понятие элементарных (типовых) звеньев как некоторых простейших составных частей динамического элемента.

Типовые звенья - это стандартные составные части динамических элементов системы, описываемые дифференциальными уравнениями не выше второго порядка. Все элементарные звенья по характеру процессов, происходящих в них, можно разбить на следующие типы: усилительное звено; интегрирующее звено; апериодическое звено; колебательное звено; дифференциальное звено первого порядка; дифференциальное звено второго порядка; звено чистого запаздывания.

) Усилительное звено. Тип звена однозначно определяется законом, связывающим между собой величину на входе - х и на выходе - у. Дляусилительного звена, которое из-за отсутствия переходных процессов иногда называют безинерционным или статическим, этот закон имеет вид: у = к∙х.

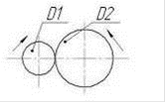
Рисунок 7.1

Переходная функция усилительного звена имеет вид: h (t) = к. Этот закон является наиболее простым и состоит в следующем преобразовании: входной сигнал умножается на постоянную величину к, называемую коэффициентом усиления. Коэффициент усиления может иметь любое действительное значение, как положительное, так и отрицательное. Ниже изображена выходная величина при скачкообразном изменении входной величины.

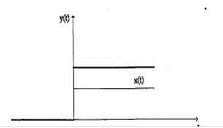
Рисунок 7.2

Передаточная функция этого звена имеет вид: W (p) = к.

) Интегрирующее звено. Интегрирующее звено характеризуется тем, что скорость изменения выходной величины пропорциональна входной величине . Переходная функция усилительного звена имеет вид:

h (t) = k-t.

Интегрирующее звено не может находиться в состоянии равновесия

при любом постоянном значении входного сигнала. Его передаточная функция

.

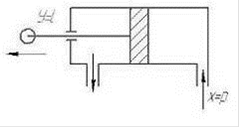
Рисунок 7.3

) Апериодическое звено. Уравнение этого звена имеет вид:

,

Где Т - постоянная времени апериодического звена, имеющая размерность времени;

к - коэффициент усиления или статический коэффициент передачи.

Переходная функция апериодического звена имеет вид:

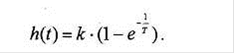
При Т=>0 и Т→ ∞ переходная функция асимптотически стремится к установившемуся значению равному к. Ее зависимость представлена на рисунке 7.4

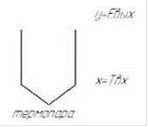
Рисунок 7.4

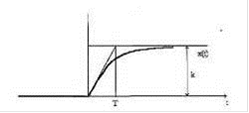
Рисунок 7.5

Передаточная функция апериодического звена:

Интересное из раздела

Электроника
Электроника. Методические указания для лабораторных работ. Составители: Е.М.Фискин, М.М.Фискина. -Иркутск: Изд-во ИрГТУ, 2012.-25 с. Содержатся мате ...

Программируемый формирователь последовательности импульсов с цифровой индикацией количества импульсов
Проектируемое устройство в готовом виде представляет собой отдельный прибор, основной функцией которого является формирование последовательности импульсов заданной частот ...

Анализ и синтез линейной системы автоматического управления
Анализ системы автоматического управления Исходные данные: Рассмотрим структурную схему III изображенную в табл. П-1.1. Параметры ...