Согласование источника с каналом

Рассмотрим принципы и предельные возможности непосредственного согласования дискретного источника сообщений с непрерывным каналом связи. Напомним, что в непрерывном канале надо знать плотности распределения случайных процессов сигналов, помех и их же условные плотности распределения. Это понятие вводится при моделировании канала связи и с точки зрения передачи сообщений нет большого противоречия в том, что источник принят дискретным, а канал непрерывный.

Будем считать канал гауссовым, то есть все статистики в нем имеют нормальное распределение. На входе канала, помимо сигнала, присутствует помеха типа «белый шум».

Предельные возможности согласования дискретного источника с непрерывным каналом определяются теоремой Шеннона.

Пропускная способность гауссова канала равна:

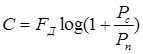. (4.2)

где FД - частота дискретизации, определенная выше. Рп ¾ мощность помехи, определяется по заданной спектральной плотности мощности N0 (дано в задании на курсовой проект) и полосе частот модулированного сигнала :

. (4.3)

По этим формулам, пользуясь неравенством Шеннона , определим РС, обеспечивающую передачу по каналу.

Для определения РС примем пропускную способность канала равную:

.

Выделим из (4.2) Рс.

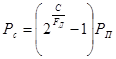,Вт. (4.4)

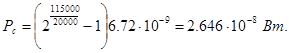
Интересное из раздела

Блок горизонтального отклонения электронно-лучевого осциллографа
Проектирование блока горизонтального отклонения электронно-лучевого индикатора предусматривает расчет следующих функциональных блоков схемы: ü Гене ...

Цифровой КИХ-фильтр для частотной селекции измерительных сигналов
Цифровой фильтр (ЦФ) - устройство, пропускающее, либо подавляющее заданные в цифровой форме сигналы в определенной полосе частот. В отличие от аналоговых фильтров, у кото ...

Цифровой УКВ-приемник
В последние несколько лет заметна тенденция резкого сокращения сроков проектирования новых изделий при все возрастающих требованиях к их качественным характеристикам. Это ...