Согласование источника информации с каналом связи

Заданный сигнал мы представили отсчетами, идущими с заданным интервалом. Такая выборка содержит полную информацию о передаваемом сигнале и, следовательно, сама представляет источник информации. Выше было определено количество выборок для одного из сигналов.

Таким образом, выборки это алфавит источника информации и вероятности букв этого алфавита равны друг другу. Такой источник имеет ряд информационных характеристик: количество информации в знаке, энтропию, производительность, избыточность. В дальнейшем нас будет интересовать производительность, которая характеризует скорость работы источника и определяется по следующей формуле:

, (7.1)

гиде - энтропия алфавита источника, бит/с;

- среднее время генерации одного знака алфавита, с.

(7.2)

Рассмотрим принципы и предельные возможности непосредственного согласования дискретного источника сообщений с непрерывным каналом связи. Напомним, что в непрерывном канале надо знать плотности распределения случайных процессов сигналов, помех и их же условные плотности распределения. Это понятие вводится при моделировании канала связи и с точки зрения передачи сообщений нет большого противоречия в том, что источник принят дискретным, а канал непрерывный. Полоса пропускания канала должна быть достаточной для прохождения спектра модулированного сигнала. Величина Dw была определена нами в разделе 5. Предельные возможности согласования дискретного источника с непрерывным каналом определяются следующей теоремой Шеннона (которая аналогична такой же дискретного источника и дискретного канала).

Теорема Шеннона

. Дискретные сообщения, выдаваемые дискретным источником с производительностью можно закодировать так, что при передаче по гауссову каналу с белым шумом, пропускная способность которого С превышает вероятность ошибки Рош может быть достигнута сколь угодно малой.

При определении пропускной способности канала статистические законы распределения помехи, сигнала, и суммы сигнала и помехи - нормальные законы с соответствующими дисперсиями Рп, Рс и Рс+Рп.

Пропускная способность гауссова канала равна:

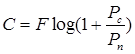, (7.3)

где F - частота дискретизации, Гц;

Рп - мощность помехи, Вт.

Определяется по заданной спектральной плотности мощности N (дано в задании на курсовой проект) и полосе частот модулированного сигнала .

, (7.4)

где N0 - спектральная плотность мощности шума.

По этим формулам, пользуясь неравенством Шеннона , надлежит определить Рс, обеспечивающую передачу по каналу.

По формулам (2.9) - (2.10) получаем:

H (a) =log2 (5,609) =2,488 бит/с;

2,488/0,0000785=31690 бит/с.

Мощность помехи:

Рп=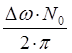; (7.5)

PП=5,73·10-11 Вт.

Мощность сигнала:

PC = (2 C·Δt - 1) ·PП; (7.6)

PC=1,785·10-9 Вт.

Интересное из раздела

Исследование аналого-цифрового и цифрового преобразователей
Аналого-цифровые преобразователи предназначены для преобразования непрерывных (аналоговых) сигналов в дискретные (цифровые), которые могут использоваться в ...

Cинтез инвертирующего усилителя
Операционные усилители в настоящее время находят широкое применение при разработке различных аналоговых и импульсных электронных устройств. Это связано с те ...

Амплитудная модуляция
Исследование различных видов модуляции необходимо для определения требуемых свойств каналов, сокращения избыточности модулированных сигналов и улучшения исп ...