Критерии устойчивости САР

Задача: Определить устойчивость системы, используя критерий Михайлова и Гурвица.

По кривой Михайлова составить характеристическое уравнение системы.

При . Определить . Сделать вывод об устойчивости системы.

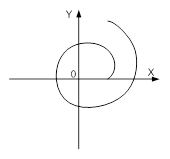
- характеристическое уравнение.

По данным задачи получим характеристическое уравнение вида:

. Проверим устойчивость системы по критерию Гурвица.

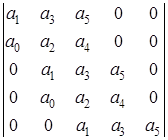- определитель Гурвица в общем виде для характеристического уравнения пятой степени.

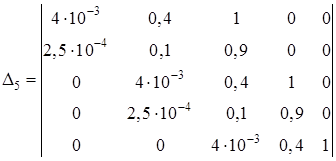- определитель Гурвица.

Система будет устойчива, если определитель Гурвица и все его диагональные миноры будут положительны.

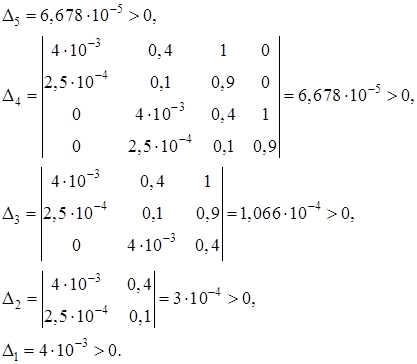
Так как определитель Гурвица и все его диагональные миноры положительны, то система устойчива.

. Проверим устойчивость системы по частотному критерию Михайлова.

)

)

)

)

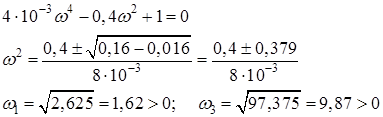
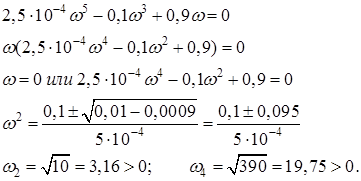
Все корни положительны и перемежающиеся, следовательно, система устойчива.

Интересное из раздела

Проект корпоративной вычислительной сети
Локальные сети в последнее время все более превращаются в обязательную принадлежность любой компании, имеющей больше одного компьютера. Это обусловлено возр ...

Блок горизонтального отклонения электронно-лучевого осциллографа
Проектирование блока горизонтального отклонения электронно-лучевого индикатора предусматривает расчет следующих функциональных блоков схемы: ü Гене ...

Организация аудиовидеконференцсвязи
В настоящее время технологии видеоконференцсвязи находятся в стадии динамичного развития во всех, без исключения, развитых странах мира. Преимущества компью ...