Аппроксимация

Находим остальные коэффициенты:

; ; ;

; ; ;

; .

Полином по степеням х находится по формуле, в которой аппроксимирующий полином в отличие от аппроксимируемой функции обозначен как :

,

где - ортогональные полиномы. Группируя коэффициенты по степеням х и собирая подобные члены, приходим к удобным выражениям для вычисления членов А0, А1х, А2х2, А3х3 и т.д. этого полинома:

;

;

;

;

;

;

.

В итоге полином по степеням х:

;

Рассматриваемый полином удовлетворяет требованиям формулы:

= 0 и х = 0 ;

Подставляем в формулу значение:

,

получаем истинный теоретический полином Во по степеням :

.

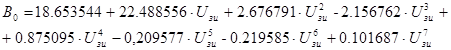По найденному уравнению вычисляем и заносим в нижнюю графу таблицы 2 значения В0 в контрольных точках напряжения смещения .

Из сопоставления экспериментальных значений и теоретических В0 рисунку 2 видим, что совпадение очень хорошее. Абсолютная ошибка находится в пределах сотых долей, что характеризует пригодность результатов аппроксимации для дальнейшего гармонического анализа различных нелинейных явлений.

Интересное из раздела

Проектирование зеркальных антенн для индивидуального приема спутниковых программ
Наибольший интерес в настоящее время представляет прием телевидения в диапазоне 11…12 ГГц, для которого наиболее применимы параболические антенны, так как п ...

Использование специализированных микропроцессоров
Рассмотрим преимущества цифровой обработки сигналов (ЦОС) на сравнении аналоговых и цифровых фильтров. Цифровые фильтры всё чаще находят своё применение в м ...

Расчет линейной электрической цепи при гармоническом воздействии
Цель курсовой работы состоит в практическом освоении методов расчета простых и сложных электрических цепей при воздействии на них гармонических колебани ...