Цифровые фильтры с конечной импульсной характеристикой (КИХ-фильтры)

Линейная фазовая характеристика КИХ-фильтра.

Пусть {h (n)} - физически реализуемая последовательность конечной длины, заданная на интервале 0. Ее z-преобразование равно:

Преобразование Фурье от {h (n)}:

(3)

является периодическим по частоте с периодом 2р.

Из уравнения (3) видно, что модуль преобразования Фурье является симметричной функцией, а фаза -антисимметричной функцией частоты, т.е.

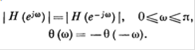(5)

На практике при расчете КИХ-фильтров часто требуется строго линейная фазовая характеристика. При этом фазовая характеристика и(щ) имеет вид:

(6)

где б - постоянная фазовая задержка, выраженная через число интервалов дискретизации.

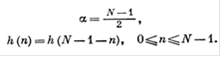(8)

Условие (7) означает, что для каждого N существует только одна фазовая задержка б, при которой может достигаться строгая линейность фазовой характеристики фильтра. Из условия (8) следует, что при заданном б, удовлетворяющем условию (7), импульсная характеристика должна обладать вполне определенной симметрией.

В зависимости от значения N (нечетные или четные) и вида симметрии импульсной характеристики (симметричная или антисимметричная характеристика) возможны четыре различных вида КИХ-фильтров с линейными фазовыми характеристиками.

Таблица1. Различие четырех типов КИХ-фильтров с линейной фазовой характеристикой

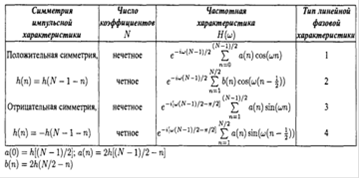
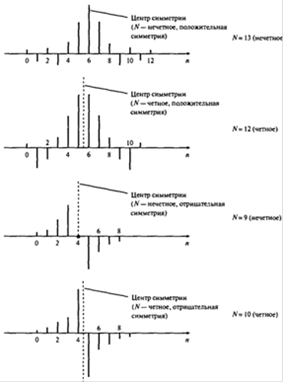
Рис.3. Коэффициенты импульсной характеристики четырех типов фильтров с линейной фазовой характеристикой

Интересное из раздела

Комплекс аппаратных средств для трансляции звукового сигнала на большие расстояния
Звук играет важную роль в жизнедеятельности человека. Каждый день мы слышим очень много разнообразных звуков, так же существует необходимость передават ...

Проект корпоративной вычислительной сети
Локальные сети в последнее время все более превращаются в обязательную принадлежность любой компании, имеющей больше одного компьютера. Это обусловлено возр ...

Цифровой УКВ-приемник
В последние несколько лет заметна тенденция резкого сокращения сроков проектирования новых изделий при все возрастающих требованиях к их качественным характеристикам. Это ...