Оценка устойчивости САР на основе критерия Михайлова

Для оценки устойчивости САР необходимо получить уравнение кривой Михайлова. Для этого воспользуемся характеристическим уравнением замкнутой системы

A(s) = (a0·sn+ a1·sn-1+ a2·sn-2+ . . . + an)=0;

Переходя в частотный диапазон, заменяя s → jω, выделяя вещественную и мнимую составляющие, получим уравнение кривой Михайлова.

D(j ω) =a0· (j ω)n + a1· (j ω)n-1 + a2· (j ω)n-2 +. . .+ an-1· (j ω) + an =

= U(ω) +jV(ω)

Где U(ω), V(ω) − вещественная и мнимая составляющие уравнения кривой Михайлова.

По уравнению кривой Михайлова, при изменении ω, на комплексной плоскости строиться кривая Михайлова (рис. 6.1)

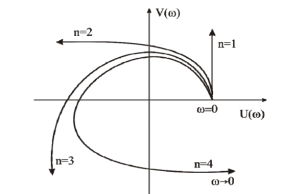
Рис. 6.1 Кривые Михайлова, построенные для устойчивых систем cn=1, n=2, n=3, n=4

Для того, чтобы САР была устойчивой необходимо и достаточно выполнение следующих условий:

- при ω=0 годограф кривой Михайлова должен начинаться на положительной вещественной оси;

-при изменении частоты 0 = ωдо ∞ годограф кривой Михайлова должен поочередно, нигде не обращаясь в 0, в положительном (против часовой стрелки) направлении пройти n квадрантов.

Если годограф кривой Михайлова при конкретной частоте, не равной 0, проходит через начало координат, то система является нейтральной.

При невыполнении хотя бы одного из сформулированных условий система является неустойчивой. Подставим известные значения an, в характеристическое уравнение замкнутой системы

A(s)=0·s4+ 0,00282·s3+ 2,618129·s2+ 114,3017·s+128,7276=0;

D(j ω) =0· (j ω)n + 0,00282· (j ω)3 + 2,618129· (j ω)2 +114,3017 ·(j ω) +

128,7276=(-2,618129· ω2 + 128,727)+j(0,00282· ω3+114,3017 · ω)

Изменяя ω можно построить кривую Михайлова (рис. 6.2, 6.3)

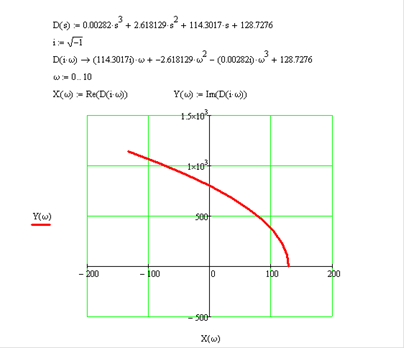
Рис. 6.2 Кривая Михайлова для ωот 0 до 10 (с-1)

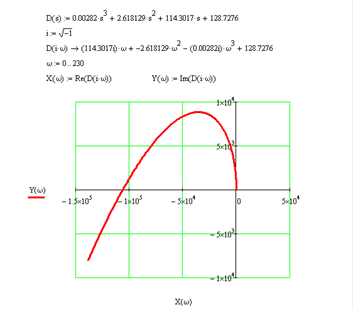
Рис. 6.3 Кривая Михайлова дляωот0 до 230 (с-1)

Вывод:

Все требования условия устойчивости Михайлова выполняются:

- при ω=0 годограф кривой Михайлова начинается на положительной вещественной оси;

-при n=3 порядок следования квадрантов не нарушается.

Следовательно, САР следящей системыс данными параметрами является устойчивой.

Интересное из раздела

Расчет параметров четырехполюсника
Системы автоматики, телемеханики и связи на железнодорожном транспорте представляют собой технические средства управления перевозочным процессом, способству ...

Моделирование цифро-аналоговых преобразователей
С введением новых телевизионных стандартов, таких как EDTV (телевидение повышенной четкости) и HDTV(телевидение высокой четкости) повышаются требования к АЦП и ЦАП. Некот ...

Устройство оперативной памяти статического типа емкостью 12 Кб для микропроцессора Intel 8080
Одним из ведущих направлений развития современной микроэлектронной элементной базы являются большие интегральные микросхемы памяти, которые служат основой д ...