Исследование и расчет цепей постоянного тока

. Освоение методики измерения токов, напряжений, потенциалов.

. Опытная проверка законов Кирхгофа и принципа наложения.

. Расчёт токов в ветвях заданной электрической цепи методами контурных токов, узловых потенциалов, эквивалентного генератора.

. Построение потенциальной диаграммы.

. Составление баланса мощностей.

. Сравнение результатов опыта и расчёта.

Законы Кирхгофа

Законы Кирхгофа являются фундаментальными законами электротехники.

Первый закон Кирхгофа формулируется для узла электрической цепи: алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю. При этом подходящие к узлу токи записываются с одним знаком, отходящие - с другим. Например, для узла, изображенного на рис. 1, можно записать первый закон Кирхгофа:

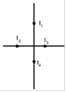
Рис. 1 Узел электрической цепи

I1 + I2 - I3 - I4 = 0 или - I1 - I2 + I3 + I4 = 0

Число линейно независимых уравнений, составляемых по первому закону Кирхгофа, на единицу меньше числа узлов схемы.

Второй закон Кирхгофа формулируется для контура электрической цепи: алгебраическая сумма падений напряжений на участках контура равна алгебраической сумме ЭДС того же контура. При этом если направление ЭДС совпадает с направлением обхода контура, то она берется со знаком „плюс", если не совпадает - со знаком „минус”. Падение напряжения на элементе берется со знаком „плюс", если направление тока в элементе совпадает с направлением обхода, если не совпадает - со знаком „минус".

Например, для контура, показанного на рис. 2, можно записать:

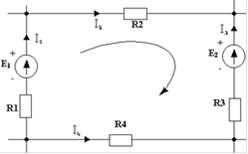
Рис. 2

I1 + R2I2 - R3I3 - R4I4 = E1 - E2

Уравнения по второму закону Кирхгофа составляются для независимых контуров - контуров, отличающихся друг от друга хотя бы одной новой ветвью.

Последовательность определения токов ветвей по законам Кирхгофа:

) Выбирается направления токов ветвей. Число токов равно числу ветвей схемы. Токи ветвей с источниками тока известны.

) Записываются уравнения по первому закону Кирхгофа, их число на единицу меньше числа узлов схемы.

) Выбираются независимые контуры и направления их обхода.

) Записываются уравнения по второму закону Кирхгофа для независимых контуров, при этом уравнения для контуров, включающих источники тока, не составляются.

) В результате совместного решения уравнений, составленных по первому и второму законам Кирхгофа, определяются токи ветвей.

Метод контурных токов

В этом методе за неизвестные принимают токи независимых контуров (контурные токи), а токи ветвей выражают через контурные.

Рассмотрим правила формирования уравнений на примере схемы, приведенной на рис. 3, в которой известны величины ЭДС и ток источника тока, а также все сопротивления.

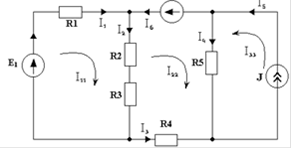
Рис. 3

Выберем независимые контуры и направления их обхода. Допустим, что в каждом контуре протекает свой контурный ток, совпадающий с направлением обхода - I11 , I22 , I33 .Выберем направления токов ветвей и составим уравнения по второму закону Кирхгофа для выбранных контуров (для контура с источником тока уравнение не составляется, так как I33 = J):

R1I1 + (R2 + R3)I2 = E1

(R2 + R3)I2 - R4I3 + R5I4 = -E2 (*)

Выразим токи ветвей через контурные:

I1 = I11 ; I2 = I11 - I22 ; I6 = I3 = -I22;= I22 + I33 ; I5 = I33 ; I33 = J ; I5 = J

и подставим в систему (*):

R1I11 + (R2 + R3)(I11 - I22) = E1

-(R2 + R3) (I11 - I22) - R4(-I22) + R5(I22 + I33) = -E2

После группировки получим:

(R1 + R2 + R3)I11 - (R2 + R3) I22 = E1

-(R2 + R3) I11 + -(R2 + R3 + R4 + R5 )I22 + R5I33 = -E2

В общем виде для трехконтурной схемы с одним источником тока:

R11I11 + R12I22 + R13I33 = E11I11 + R22I22 + R23I23 = E22,

где R11 , R22 - собственные сопротивления контуров I11 и I22, каждое из которых равно сумме сопротивлении, входящих в данный контур;

R12 = R21 , R13 ,R23 - общие сопротивления контуров. Общее сопротивление равно сопротивлению ветви, общей для рассматриваемых контуров, Общие сопротивления берутся со знаком “плюс”, если контурные токи в них направлены одинаково и со знаком “минус”, если контурные токи в них направлены встречно. Если контуры не имеют общей ветви, то их общее сопротивление равно нулю. В рассматриваемом примере R13 = 0;

Интересное из раздела

Cинтез инвертирующего усилителя
Операционные усилители в настоящее время находят широкое применение при разработке различных аналоговых и импульсных электронных устройств. Это связано с те ...

Повышение технологичности печатного узла усилителя на ОУ
Целью данного курсового проекта является повышение технологичности печатного узла усилителя на ОУ за счет применения прогрессивных методов монтажа SMD-к ...

Проводные линии электросвязи
Проводные линии электросвязи делятся на кабельные, воздушные и оптоволоконные. Линии электросвязи возникли одновременно с появлением электрического теле ...