Синтез двухэлементного ДП Z1.

Учитывая, что p=jw, получим в классической форме записи функцию сопротивления ДП Z1(см. (1.1)):

1(p)= , (1.3)

Заменяем оператор р на jw получаем:

Z1(jw)=, (1.4)

Рассчитаем нули функции Z1(p), приравняв числитель функции к нулю:

= 0

Найдём корни уравнения:

w01 = 0 с-1; w02 = 14142 с-1; w03 = -14142 с-1

Далее найдём полюсы:

= 0

Найдём корни уравнения:

w¥1 = -8364 с-1; w¥2 = 8364 с-1; w¥3 = -28566 с-1; w¥4 = 28566 с-1.

Построим полюсно-нулевое изображение и характеристическую строку.

По выражению (1.3) видим, что ДП Z1(jw) класса «0 - 0» имеет два резонанса токов:

; .

Так же двухполюсник имеет один резонанс напряжений:

.

Реализуем по схеме Фостера 1-го рода методом разложения на простые дроби:

. (1.5)

= 1742627,

= 8257372.

C1= = 1/1742627 = 5,738×10-7Ф.

Из условия резонанса:

.

С3= = 1/8257372 = 12,11 мкФ.

Из условия резонанса:

.

Частотная зависимость сопротивления ДП сведена в табл. 1.1. График частотной зависимости Z1 (w) представлен на рисунке 1.3.

Таблица 1.1. Частотная зависимость сопротивлений двухполюсника Z1

Схемы и параметры первого ДП.

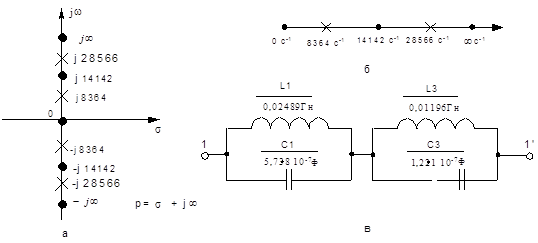
Интересное из раздела

Амплитудная модуляция
Исследование различных видов модуляции необходимо для определения требуемых свойств каналов, сокращения избыточности модулированных сигналов и улучшения исп ...

Расчет характеристик сигналов и каналов связи
В последнее десятилетие ХХ века произошла научно-техническая революция в области транспортной связи, в основе которой лежат два крупных достижения ...

Функционально-структурный анализ системы автоматического управления (регулирования) технического объекта
Работа любого технологического объекта характеризуется различными параметрами, которые изменяются в зависимости от работы машины и воздействия внешних факто ...