По заданным корням характеристического уравнения записать общее решение однородного дифференциального уравнения, определить , указать расположение корней на плоскости и по их расположению отметить х

Система будет находиться на границе устойчивости

при наличии:

. Нулевого корня.

Система будет устойчивой не относительно регулируемой величины , а относительно её скорости изменения . Такую систему называют нейтрально устойчивой

, имея в виду её безразличие к значению самой регулируемой величины.

. Пары чисто мнимых корней.

Граница устойчивости второго типа называется колебательной границей устойчивости

. Система будет иметь незатухающие гармонические колебания с постоянной амплитудой.

Пример:

, ,

Общее решение дифференциального уравнения

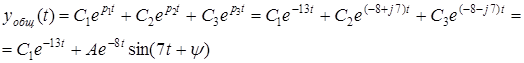
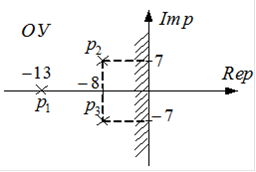
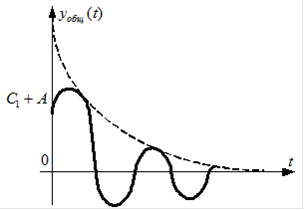
Характер переходного процесса немонотонный.

Корни характеристического уравнения находятся в левой полуплоскости. Система устойчива.

Интересное из раздела

Функционально-структурный анализ системы автоматического управления (регулирования) технического объекта
Работа любого технологического объекта характеризуется различными параметрами, которые изменяются в зависимости от работы машины и воздействия внешних факто ...

Проектирование генераторного триода дециметрового диапазона
Генераторные лампы предназначены для генерирования и усиления электрических колебаний низких и высоких частот. По роду работы генераторные лампы можно разде ...

Цифровая обработка сигналов
Развитие телекоммуникационных сетей увеличивает роль и значение передачи дискретных сообщений в электросвязи. Целью дисциплины ТЦС является: · изложение п ...