Метод частотной выборки

Используя выражение (21), приведем (19) к виду (для четного N)

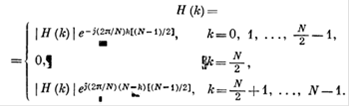(22)

Подставив выражение для H(k) в (18) и сократив члены, получим:

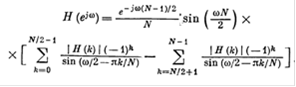(23)

Подстановка l = N - к во вторую сумму выражения (23) дает:

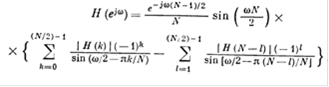(24)

Объединяя члены и учитывая формулу (20), находим

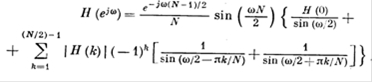(25)

Используя тригонометрические тождества, получаем искомый результат:

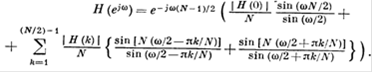(26)

Выражение (26) без учета множителя представляет искомую действительную функцию для фильтра вида 1 с частотной выборкой, имеющего линейную фазу и четное N.

Аналогичные выкладки для фильтра и нечетного N дают:

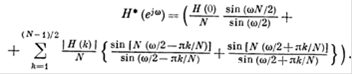(27)

. Моделирование КИХ-фильтров в MathCAD

. ФНЧ

Число отсчетов импульсной характеристики N - четное.

Задаем частоту среза:

Модуль идеальной периодической частотной характеристики имеет вид:

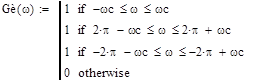
Поставим вместо непрерывной функции дискретные отсчеты.

Дискретизируем эту характеристику в N=16 точках на интервале 0≤щ≤2р. Зададим отсчеты в переходной полосе G2 и G14.

Запишем выражение для линейной фазовой характеристики:

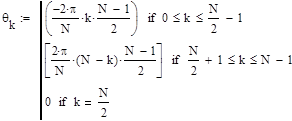
Фазовая характеристика:

Искомую конечную импульсную характеристику получим на основе ОДПФ в виде:

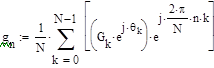
Импульсная характеристика:

Интерполяционная формула для восстановления частотной характеристики реального фильтра по N отсчетам частотной характеристики идеального фильтра имеет вид:

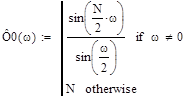
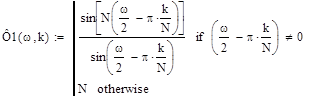
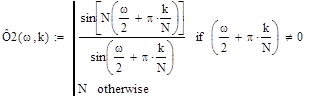
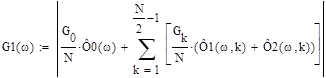
Интересное из раздела

Расчет параметров различных видов сигналов
В последнее десятилетие ХХ века произошла научно-техническая революция в области транспортной связи, в основе которой лежат два крупных достижения науки сер ...

Калибровка мониторов на основе науки о цвете – колориметрии
Полиграфическая индустрия активно развивается и предлагает клиентам все больше новых и интересных решений. Также растет требовательность заказчиков к резуль ...

Проектирование зеркальных антенн для индивидуального приема спутниковых программ
Наибольший интерес в настоящее время представляет прием телевидения в диапазоне 11…12 ГГц, для которого наиболее применимы параболические антенны, так как п ...