Метод частотной выборки

Хорошо известны три класса методов расчета КИХ-фильтров с линейной фазой: методы взвешивания с помощью окна, методы частотной выборки, а также методы расчета оптимальных (по Чебышеву) фильтров.

Метод взвешивания предоставляет простой и гибкий способ вычисления коэффициентов КИХ-фильтра, но не позволяет разработчику адекватно управлять параметрами фильтра. Достоинством метода частотной выборки является то, что он допускает рекурсивную реализацию КИХ-фильтров, что может быть вычислительно выгодно. Но данному методу недостает гибкости в плане управления или задания параметров фильтров. Также, в настоящее время широко используется оптимальный метод, который в большинстве случаев дает требуемый КИХ-фильтр.

Рассмотрим подробнее метод частотной выборки.

КИХ-фильтр может быть однозначно задан, как коэффициентами импульсной характеристики {h(n)}, так и коэффициентами ДПФ импульсной характеристики {Н(k)}. Обе эти последовательности связаны соотношениями:

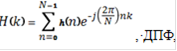, ДПФ, (9)

, ОДПФ. (10)

Кроме того, известно, что коэффициенты ДПФ КИХ-последова-тельности, равные Н (k), можно рассматривать как значения z-преобразования импульсной характеристики фильтра, найденные в N равноотстоящих точках на единичной окружности, т. е.

Н(k) = Н (z) |z= (11)

Таким образом, z-преобразование импульсной характеристики КИХ-фильтра можно легко выразить через коэффициенты ДПФ его импульсной характеристики:

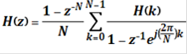(12)

Из соотношения (12) следует, что для аппроксимации произвольной непрерывной частотной характеристики следует произвести ее дискретизацию по частоте в N равноотстоящих точках (взять частотную выборку) и найти непрерывную частотную характеристику, интерполируя отсчеты частотной характеристики. В этом случае ошибка аппроксимации на частотах взятия выборки будет в точности равна нулю и иметь конечную величину в промежуточных точках. Чем более гладкой является аппроксимируемая частотная характеристика, тем меньше ошибка аппроксимации между частотными отсчетами.

Описанную процедуру можно было бы использовать непосредственно для расчета КИХ-фильтров, однако для улучшения качества аппроксимации, т. е. для уменьшения ошибки аппроксимации, часть частотных отсчетов целесообразно сделать независимыми переменными. Значения этих независимых переменных обычно рассчитывают методами оптимизации на вычислительной машине таким образом, чтобы минимизировать некоторую простую функцию ошибки аппроксимации. В качестве независимых переменных можно выбрать частотные отсчеты, расположенные в переходной полосе между двумя полосами, внутри которых частотная характеристика определена (т. е. в случае фильтра нижних частот между полосами пропускания и непропускания).

Чтобы понять, почему при такой методике оптимизации часто лишь несколько из N частотных отсчетов могут существенно уменьшить ошибку аппроксимации, необходимо вычислить значения Н (z) на единичной окружности. Получаемая при этом интерполяционная формула для расчета частотной характеристики фильтра в функции непрерывной частоты имеет вид:

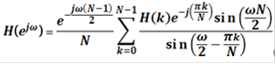(13)

Отсюда следует, что частотная характеристика фильтра является линейной комбинацией частотных интерполирующих функций вида

Интересное из раздела

Электроника
Электроника. Методические указания для лабораторных работ. Составители: Е.М.Фискин, М.М.Фискина. -Иркутск: Изд-во ИрГТУ, 2012.-25 с. Содержатся мате ...

Автоматизация судовой энергетической установки
Автоматическое управление технологическими процессами является одним из главных направлений научно-технического прогресса на морском транспорте. Автоматизация СЭУ обеспе ...

Источник питания охранного устройства
В настоящее время существует множество систем, предназначенных для осуществления охраны и безопасности объектов. С развитием науки и техники у ...